Calculating sound delay in bpm for anywhere on the marching field!
Note: This post has been condensed into a dynamic formula that can be found here. Enjoy!
This is a project that has taken me awhile to work out the math and create a formula that works for both distance and bpm at the same time, and I’m very excited to begin to write about it! In the future I’ll also be writing about Cost Of Dynamic which is similar to this article, but in terms of volume. But first, let me explain what any of this means since I think I might have lost some of you already.
Cost Of Timing is an easy way to say “speed of sound effecting rhythm at distances on the football field.” Basically I’ve derived a mathematical equation that supplies you with either the tempo or the distance at which the sound delay will change the arrival of a note (as heard from the audience’s perspective). Don’t worry, the math is easy, but you do need to know at least one variable to plug in which will allow you to get the correct output. And before you decide what variable to use you’ll also need to know what rhythm, or note duration, that you are calculating for.
Just so we’re on the same page, there’s three reasons you’d want to use these formulas on the field. #1 is that you’re just curious what the denomination of the sound delay is at certain places on the field and at certain tempos. #2 is that you’re trying to enter in time with the front ensemble from the back portion of the field and need to know exactly how early to play ahead of them for it to be in time up front. #3 is that you’re arranging some crazy music that aligns or splits based on certain parts of the field that normally could not possibly be played in time without the formula. If there’s a #4 it hasn’t been figured out yet and would need someone with a lot of experience to push this idea even further! The Number three idea is what interests me the most, one and two are just a byproduct of figuring out these formulas. My personal goal with these formulas is to compose actual music that has individual parts play off each other from seemingly impossible spots on the field.
Before we get into the meat and potatoes of the formulas below, let’s start in three dimensional space, on the playing field. Let’s just assume you have a drummer positioned on the back sideline and you want them to play a note with someone positioned on the front sideline. You may have seen demonstrations like this, and hopefully you know that in the marching band world you’ll need the drummer that is furthest back to establish the tempo and for the performer at the front to listen back and play with them. This is obviously due to the speed of sound (for the math below we’re assuming the sound is traveling through air and that you’re at sea level at a nice 68 °F and also that your audience member is sitting in front of the 50 yard line on center). Now, what if we reverse everything? What if the member at the front establishes the tempo and the drummer in the back listens forward for timing? We should also know now that the sound from the front would arrive to the audience before the sound at the back, even though the drummer at the back hears them in unison. But the question these formulas will solve is how far off will these notes be at certain tempos.
Now, you might be asking yourself, well why do I care what note value that was when I’ll never establish tempo at the front of the field anyway? And you might be right, if you’re just trying to get through the marching band or drum corps season you won’t want to try anything crazy, and yes, this is crazy. But… What if you could calculate that delay for any rhythm and then arrange a music phrase where tempo was established from the front 50 yard line and any member of the group could play in time with that sound no matter where they were on the field? Would you be pushing the envelope and innovating the activity in a way that until now has never been done before? Yes. Yes you would be.
Imagine for a second that you have a band with members standing in pods at the back 2 corners of the field while the front ensemble plays a melody. Then all of a sudden the members in the back begin playing stab notes in time with the pit. If the audience and judges understand the physics behind that you might be on the receiving end of some serious credit! And that’s just the beginning, anyone that can push this formula to the max and wring it out for all its worth might be able to create something even more incredible. So let’s dive in.
(For the record, these formulas use standard beats per minute (bpm) for timing and feet (ft) for distance. For outdoor use you’ll want to convert the results to yards by dividing it by 3. For indoor reference all standard basketball courts are 50ft from sideline to sideline.)
Keep in mind as you read through these calculations that you only need to determine the distance up to the closest member to the audience. Once the sound arrives to them it will travel together to the audience no matter how far away the audience is from that frontmost performer (within reason, different wavelengths travel at different speeds over great distances).
Now, as stated above, you’ll need to either know ahead of time what tempo is being played, or the distance the member is performing from the front of the field (at the 50). So there’s two formulas you’ll find yourself solving for the answers. Let’s start with 8th notes. The formula for finding both of the above variables is as follows:
For 8th-notes:
Tempo = (16,800 ÷ Distance) × 2
Known distance: use this to calculate the tempo.
Distance = (16,800 ÷ Tempo) × 2
Known tempo: use this to calculate the distance.
So, if you know the tempo of the song punch that BPM into the second formula. For example, if the song is 160bpm and you want to know how far away a 16th note will sound you plug that in as (16800÷160)x2 which equals 210 feet. In order for the speed of sound to create an 8th note separation your member at the back would have to stand exactly 210 feet or 70 yards away from the tempo established at the front. Not super realistic, so let’s dig in a bit further. We’ll either have to play faster rhythms if we want this to work with our members all on the same football field, or we have to move off of the 50 yard line.
This is where some musical mathematicians will have to start calculating a little trigonometry with right triangles! For this example we know the hypotenuse needs to be 210 feet, and we also know an American football field is 160 feet wide (Canadian fields are 195 feet wide). From that we can calculate how far off to the side the member needs to stand if they were to be on the back sideline.
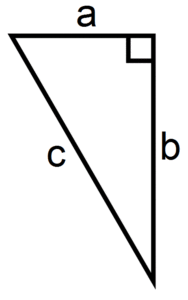
If you don’t already know the Pythagorean Theorem we can break it down to a single equation for our needs here. a²+b²=c² is the basis of what we’re doing, but we already know b and c, we’re actually looking for the side a distance, so we would use this version of the formula instead:
To find a:
a = √(c² – b²)
Find out how far off center to stand.
Now, using the numbers we already know from above, we’re going to get some big values for the squares, but don’t let it scare you, this get’s easier I promise! First, c=210 which when squared is 44,100. Second, b=160 which when squared is 25,600. Now we subtract b from c which is 18,500. And finally, when we calculate the square root of that number we get a reasonable 136.01. So distance a=136.01 feet or 45.34 yards. This finally means that our member would have to be standing a little over 45 yards from the center 50 yard line, which would put them at about the 4 yard line on either side.
That was the long way of saying the back member would have to stand on the back sideline at the 4 yard line and play his note an 8th-note ahead of the front member on the front sideline at the 50. From the audience perspective that would sound like they are play exactly together.
Side note: If you wanted your bass drummers to split 16th-notes perfectly across the field at 160bpm you could put bass 1 on the front sideline at the 50, and put bass 2 on the back sideline at the 4 yard line and just have bass 1 tap off and play 8th-notes. All bass 2 has to do is play his notes exactly in unison with bass 1 [from his perspective] and the audience will hear perfect 16th-notes split exactly. Now, change the tempo or distance and you can split faster note values anywhere on the field! Read on…
Now, this all might get a little less complicated if we start with the drill. What if we know where the members are already standing and we just want to pick a tempo that works. Well then, we’ll just start using the first formula instead of the second!
Let’s go back to both performers standing on the 50 yard line, one at the front sideline and the other at the back sideline. We know that’s 160 feet from the example above. But now we want to discover what tempo we need to play to make a note value work for us. So again first, let’s use the basic formula for 8th notes, but this time we use the top formula…
16800÷160=105bpm. This says that in order for the members to play an 8th-note difference from front to back sidelines the tempo would have to be 105bpm.
We can also use the Pythagorean Theorem to calculate the distance of a hypotenuse for when we already know the latitude and longitude of our performer, which allows them to be anywhere on the field (we can simply modify the tempo to suit their current position). The easy example is that our rear musician is standing on the back sideline, and let’s choose the 30 yard line for this example. So side b is 160ft and side a is 60ft (20 yards – since the 30 yard line is 20 yards away from center). In this situation we’ll use the following version of the formula:
To find c:
c = √(a² + b²)
Find the current distance to the front sideline at center.
Let’s plug in the values to find c. a=60 and when squared that’s 3,600. b=160 which when squared is 25,600. Add those results together for 29,200 and square root them for an answer of 170.88ft which means the member who was already standing on the back sideline and on the 30 yard line is about 171ft away from the front sideline at the 50. So you can now use 171 as the distance in our Cost Of Timing formula to calculate the delay they’ll experience at that specific spot on the field!
In all of these example’s we’ve been using the back sideline a lot, for simplicity. But in reality we don’t find our musicians on the back sideline all too often. So we can dissect the field a little more using the same information above. In fact, I’ve already done that for you! See the list below for some common examples on the field for distances and tempos.
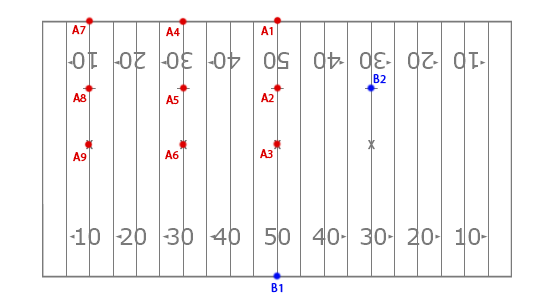
From B1:
| To Dot | Distance (ft) | 16th-note (bpm) | 8th-note (bpm) |
|---|---|---|---|
| A1 | 160 | 105 | 210 |
| A2 | 107 | 157 | – |
| A3 | 80 | 210 | – |
| A4 | 170.88 | 98.3 | 196.6 |
| A5 | 122.67 | 136.95 | – |
| A6 | 100 | 168 | – |
| A7 | 200 | 84 | 168 |
| A8 | 160.77 | 104.5 | 209 |
| A9 | 144.22 | 116.5 | 233 |
From B2:
| To Dot | Distance (ft) | 16th-note (bpm) | 8th-note (bpm) |
|---|---|---|---|
| B1 | 122.67 | 136.95 | – |
| A5 | 120 | 140 | – |
As you may have worked out from the second table, you can use these calculations to determine sound delay to the front of the field, but you can also determine the delay between players standing at distances side-to-side! Using the formulas above and below you can now calculate the Cost Of Timing from any 2 points on the field in any orientation. The most common one is from the point of view of the audience at the front of the field, but I’m sure some clever person will find a way to use this information in an unexpected way!
And now it’s your turn to customize these formulas for your own needs. below is every formula you might possibly need for different note values! This is the list to save as the formulas above are included, this is the master list:
For Quarter-notes:
Tempo = (16,800 ÷ Distance) × 4
Known distance: use this to calculate the tempo.
Distance = (16,800 ÷ Tempo) × 4
Known tempo: use this to calculate the distance.
For Quarter-note-triplets:
Tempo = (16,800 ÷ Distance) × 2.666
Known distance: use this to calculate the tempo.
Distance = (16,800 ÷ Tempo) × 2.666
Known tempo: use this to calculate the distance.
For 8th-notes:
Tempo = (16,800 ÷ Distance) × 2
Known distance: use this to calculate the tempo.
Distance = (16,800 ÷ Tempo) × 2
Known tempo: use this to calculate the distance.
For 8th-note-triplets:
Tempo = (16,800 ÷ Distance) × 1.333
Known distance: use this to calculate the tempo.
Distance = (16,800 ÷ Tempo) × 1.333
Known tempo: use this to calculate the distance.
For 16th-notes:
Tempo = (16,800 ÷ Distance) × 1
Known distance: use this to calculate the tempo.
Distance = (16,800 ÷ Tempo) × 1
Known tempo: use this to calculate the distance.
For 16th-note-triplets:
Tempo = (16,800 ÷ Distance) × 0.666
Known distance: use this to calculate the tempo.
Distance = (16,800 ÷ Tempo) × 0.666
Known tempo: use this to calculate the distance.
For 32nd-notes:
Tempo = (16,800 ÷ Distance) × 0.5
Known distance: use this to calculate the tempo.
Distance = (16,800 ÷ Tempo) × 0.5
Known tempo: use this to calculate the distance.
Go out now and run some experiments with your groups during a water break! Keep in mind if you’re using groups of players you’ll need to keep them as close together as possible, and you’ll need to do these calculations for the furthest forward person in the center of the group. While experimenting with this its probably easiest to start with snare drummers since their sound is very staccato and high frequency, they are great guinea pigs! Plus, if your goal is to enter with the front ensemble from the back of the field they’ll already be used to doing this, but you can now define precisely how much ahead of what they hear they’ll need to play. Final example: The snare drummer needs to enter with a pit phrase up front while the snares are way in the back.
If you do these calculations correctly you’ll be able to tell the center snare to subdivide an exact note value ahead of the music they hear to have a perfect entrance with the music! You can then do this with any performers far back on the field!
I’m looking forward to composing some music that utilizes these formulas for certain places on the field. I may even be able to create a web app that automatically spits out the info you need on the fly so you’re not doing any calculations yourself. In real time you can stand on the field and it’ll tell you the info you need! Look for that update sometime in the future!
Cost Of Timing is a handy calculation for very specific uses. But it will go hand in hand with Cost Of Dynamic which is the concept of volume deterioration over distance. For example, two drummers spread over a large distance will not sound the same because the closer drum will always be louder if they play the same dynamic. Look for the Cost Of Dynamic in a future article coming soon!
To save you some time check out my Sound Delay Calculator web app that does all the calculations for you!
Save this web app to your phone’s home screen for fast access to reference on the field!



